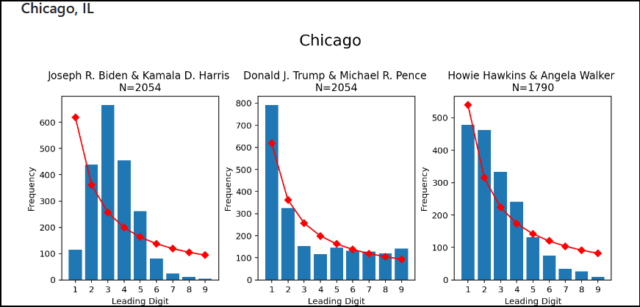
VALGFUSK Benfords lov er en matematisk lov som brukes til å bekjempe lovbrudd og manipulerte prosesser. Beregninger med modellen viser at Demokratene i USA har bedrevet omfattende valgfusk.
Politikere lyver ofte, men det gjør ikke matematikk. Benfords lov, også kalt Newcomb–Benford-loven, loven om avvikende tall, eller «første sifre-loven», er en iakttagelse om frekvensfordelingen av ledende sifre i mange virkelige oppsetninger av numeriske data.
Benfords lov brukes for utallige antall grunner av forsikringsselskaper for å avsløre bedragerier, av politiet for å avsløre lovbrudd, skatteverket for å avsløre skattesvindel, med mer.
Forenklet kan det sies at Benfords lov viser at i naturlig forekommende samlinger av tall, er det ledende tallet sannsynligvis lite.
Til for eksempel bildeanalyse, kan man med Benfords lov måle forekomsten av et bildes fargeinnhold og bildeelementforekomst, og sammenligne utfallet med hvordan bildet skal se ut ifølge Benfords lov. Om et bildes komponenter på en avgjørende måte avviker fra Benfordfordelingen, forstår man at bildet er manipulert.
Om dette forteller programlederen Latif Nasser i fjerde episoden av den amerikanske vitenskapsdokumentarserien Connected: The Hidden Science of Everything, kapittel «Digits» (serien finnes også svensktekstet hos kommersielle videostrømningstjenster):
Om en stor datamengde avviker mye fra Benfords lov, kan det være en indikasjon på at sifrene kan være oppdiktet eller manipulerte. Dette gjør loven praktisk anvendbar for kontroll innen mange forskjellige områder. For eksempel er loven anvendelig ved økonomiske regnskap, prislister, antall stemmer ved avstemminger mellom et stort antall alternativer, som med mange presidentkandidater og senatorer, samt folkemengde i byer.
Om sifrene ble fordelt enhetlig, skulle hvert tall oppstå rundt 11,1 prosent av gangene. Benfords lov gjør også forutsigelser om fordelingen av andre sifre, tredje sifre, tallkombinasjoner, og så videre.
Enkelt kan det sies, at i oppsetninger som lyder loven, vises tallet 1 som det ledende signifikante sifferet i omlag 30 prosent av tilfellene, mens 9 forekommer med mindre enn fem prosent frekvens.
Loven sier for eksempel at tallet 1 bør være førstetallet i 30,1 prosent av tilfellene, tallet 2 i 17,6 prosent av tilfellene og tallet 9 i 4,6 prosent av tilfellene i en stor datamengde.
Wikipedia endrer seg – massemedia tier
Den engelskspråkelige Wikipediasiden om Benfords lov ble redigert på lørdag, én dag etter det at dataene ble publisert som ligger til grunn for Benfordsberegningene bak de grafene som denne artikkelen lenker til.
Den 15. januar beskrev Wikipedias artikkel hvordan Benfords lov ble anvendt for å avsløre valgfusk i Iran, mens artikkelen samtidig anga at «andre eksperter» anser at Benfords lov er ubrukelig ved valgfusksanalyser.
I artikkelen, som Wikipedia redigerte på lørdag, nevnes det ikke lenger at metoden ble brukt for å avsløre valgfusk i Iran. Nå står det at metoden ikke er «idiotsikker» og at tre navngitte statsvitere – altså ikke matematikere eller personer som driver med statistikk – anser at metoden er «problematisk» og «villedende» ved studier av valgfusk.
Likevel brukes Benfords lov veldig flittig ved akkurat undersøkelser av bedrageri. Som Latif Nasser forteller i sin dokumentarserie presentert ovenfor, er beregningsmetoden så kraftfull «at den amerikanske regjeringen ikke ens vil at vi skal kjenne til den», hvilket for eksempel gjelder det «amerikanske» skatteverket IRS.
Men de studiene som har vært presentert av hittil talte stemmer viser at Joe Biden har vunnet folkets stemmer ved omfattende valgfusk.
Om amerikanske myndigheter, politikere eller massemedia kommer til å bry seg om de matematiske indisiene og bevisene på valgfusk til Joe Bidens fordel, er et helt annet spørsmål som fremtiden må utvise.








